Monte Carlo estimation of pi

Monte Carlo simulations rely on using randomness to solve problems that might be deterministic in principle and are an incredible powerful tool as modern computing power increases (and becomes cheaper!).

So how can we use Monte Carlo simulations to get an estimate for pi?

First we randomly sample points in a 2D square domain (where the side lengths = 1). If we imagine a circle (or quarter circle as we have simulated here) with radius = 1 inscribed in the square, then by calculating the ratio of points that fall within this as a proportion of the total number of points then we have an estimate for pi! Remembering to multiply by 4 as we’ve modelled a quarter circle.

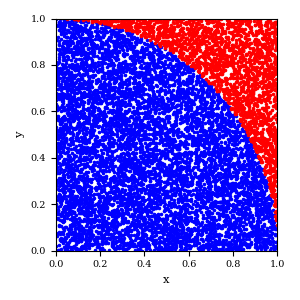
Now, how sensitive is this estimate on the number of sampled points? See below…

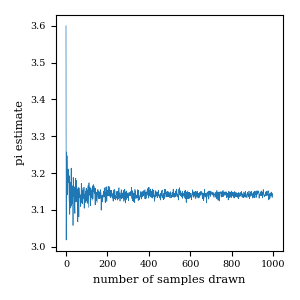
This is a fairly simple introduction to Monte Carlo simulations, an incredible powerful tool to understand.

import numpy as np
import random as r
import matplotlib.pyplot as plt
import os

def PiMonteCarlo(n):
    
    x = np.random.rand(n)
    y = np.random.rand(n)
    r = np.sqrt(np.add(np.power(x,2),np.power(y,2)))
    
    inside = len(np.where(r<1)[0])
    ratio = inside/n
    
    indin = np.where(r<1)[0]
    indout = np.where(r>=1)[0]
    return ratio*4, x, y, r, indin, indout

n = np.linspace(start = 10, stop = 100000, num = 1000, dtype = int)
pis = []
for i in range(len(n)):
    pi, x,y,r, indin, indout = PiMonteCarlo(n[i])
    pis.append(pi)
pis = np.asarray(pis)